Estimating the sparse inverse covariance matrix (precision matrix) by Graphical Lasso (with Python implementation)

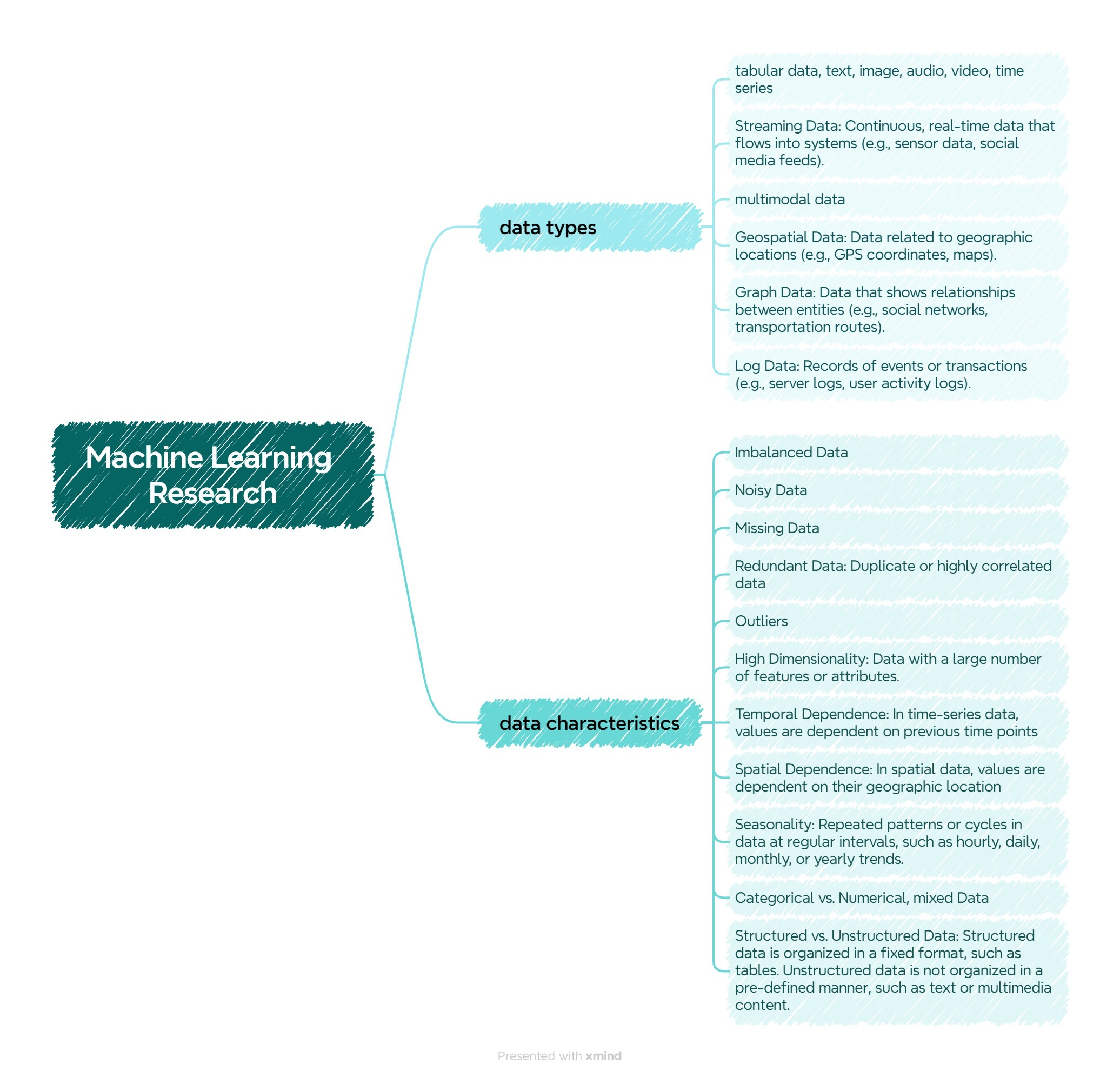
Graphical Lasso, also known as GLasso, is a statistical technique used for estimating the sparse inverse covariance matrix (precision matrix) of a multivariate Gaussian distribution. Here, Sparsity means that many elements of the matrix are zero, indicating that many variables are conditionally independent given the others.

The key idea behind Graphical Lasso is to encourage sparsity in the precision matrix, which helps in understanding the conditional dependencies between the variables.

Why Use Graphical Lasso?

1. Interpretability: Sparse precision matrices are easier to interpret because they highlight the most significant relationships between variables.
2. Overfitting Prevention: Regularizing the precision matrix helps to prevent overfitting, especially when the number of observations is small relative to the number of variables.
3. High-Dimensional Data: Useful in situations where the number of variables (features) is large compared to the number of observations.

How It Works

Graphical Lasso solves the following optimization problem:

where:

• is the precision matrix to be estimated.
• is the empirical covariance matrix of the data.
• is the L1 norm (sum of absolute values of the elements of ), which induces sparsity.
• is a regularization parameter controlling the sparsity level.

Implementation in Python

Here is an example of how to use Graphical Lasso in Python with Scikit-learn:

from sklearn.covariance import GraphicalLasso

# Assuming X is your data matrix
model = GraphicalLasso(alpha=0.1)
estimated = model.fit(X)
np.around(estimated.covariance_, decimals=3)

Graphical Lasso where input is the data matrix

Now, suppose that we already have an estimate of the covariance matrix, we can also use that as the input to the function to estimate the precision matrix. Note that sklearn must be version at least 1.3 for this to work

To upgrade sklearn by pip: pip install -U scikit-learn

Upgrade by conda: conda install scikit-learn

import numpy as np
from sklearn.covariance import GraphicalLasso
# example covariance matrix 
true_cov = np.array([[0.8, 0.0, 0.2, 0.0],
                     [0.0, 0.4, 0.0, 0.0],
                     [0.2, 0.0, 0.3, 0.1],
                     [0.0, 0.0, 0.1, 0.7]])

estimated = GraphicalLasso(covariance = 'precomputed').fit(true_cov)
np.around(estimated.covariance_, decimals=3)

# output
array([[0.8 , 0.  , 0.19, 0.01],
       [0.  , 0.4 , 0.  , 0.  ],
       [0.19, 0.  , 0.3 , 0.09],
       [0.01, 0.  , 0.09, 0.7 ]])