Subscribe to get access
??Subscribe to read the rest of the comics, the fun you can’t miss ??
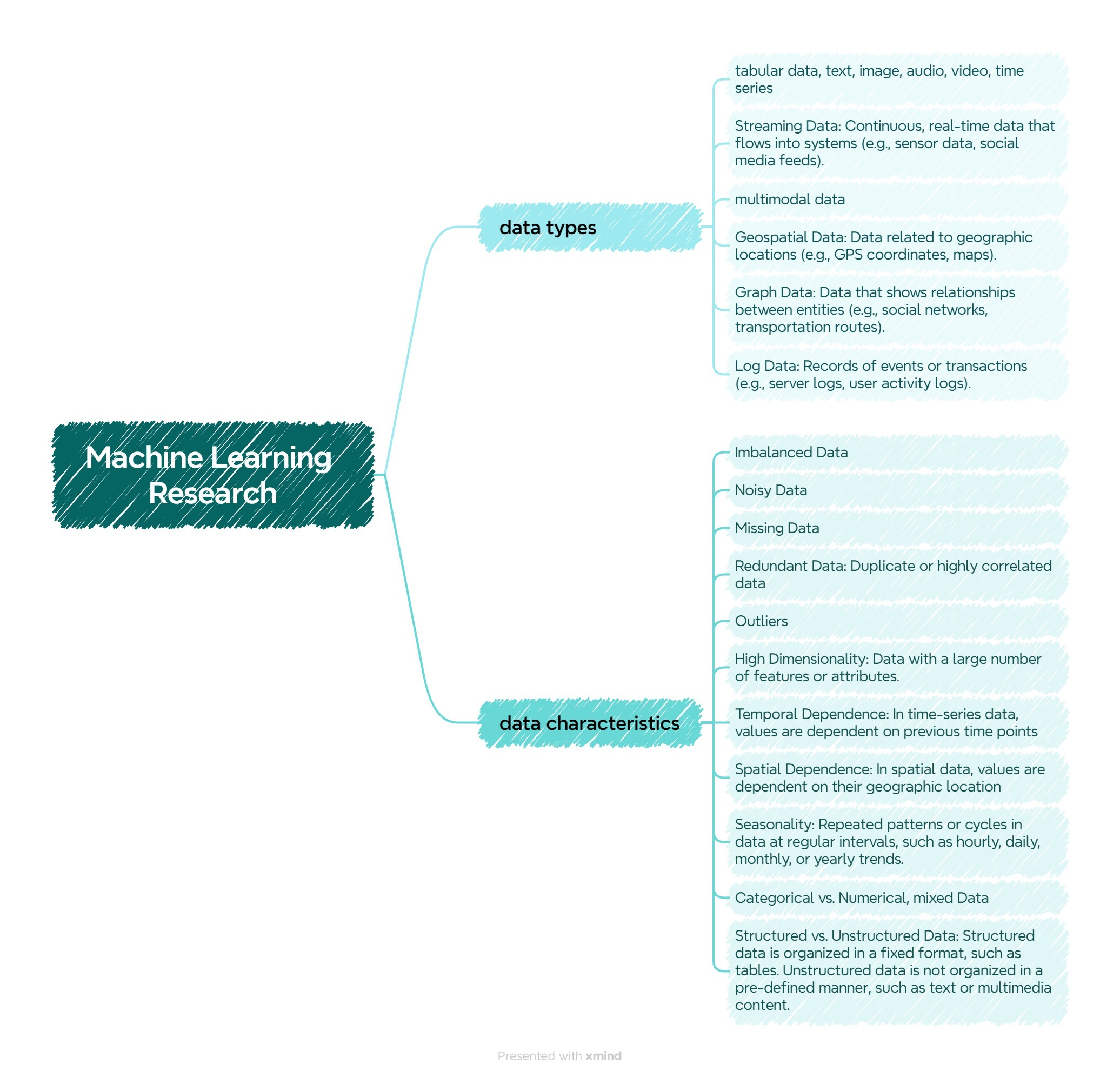
The motivation behind using multiple linear regression lies in its ability to model the relationship between multiple independent variables and a single dependent variable. By incorporating more than one predictor, this method allows for a more comprehensive analysis of how each variable contributes to the outcome. This can be particularly useful in scenarios where the outcome is influenced by a combination of factors, as multiple linear regression can provide insights into the relative impact of each variable.
What’s the general form of a multiple regression equation?
Subscribe to get access
Read more of this content when you subscribe today.
The general form of a multiple linear regression model can be written as:
Where:
is the dependent variable (the variable we are trying to predict).
are the independent variables (also called predictors or features).
is the intercept (the value of
when all independent variables are 0).
are the coefficients associated with each independent variable
. They represent the change in
for a one-unit change in the corresponding independent variable, holding all others constant.
is the error term (captures the difference between the actual value of
and the predicted value from the model).
The equation assumes a linear relationship between the dependent variable and the independent variables.
Subscribe to get access
Read more of this content when you subscribe today.
An example in Python & R
example + codes in Python (expand to see)
Let’s use the California Housing dataset, which is available through scikit-learn. It contains information about various housing features in California, such as median income, house age, population, and more, along with the median house value (the target variable).
Here’s an example using this dataset with multiple linear regression in Python:
- Import Required Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Load the dataset
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['MedHouseVal'] = data.target # Target variable (median house value)
# Display first few rows of the dataset
df.head()- Perform Exploratory Data Analysis (EDA)
# Summary statistics
print(df.describe())
# Check for missing values
print(df.isnull().sum())
# Visualize relationships between features and target
sns.pairplot(df, x_vars=df.columns[:-1], y_vars='MedHouseVal', height=2.5, aspect=0.7)
plt.show()- Split the Data into Training and Testing Sets
# Define the features (independent variables) and target (dependent variable)
X = df.drop('MedHouseVal', axis=1) # Features
y = df['MedHouseVal'] # Target
# Split the data (80% training, 20% testing)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
print(f'Training data: {X_train.shape}, Testing data: {X_test.shape}')- Train a Multiple Linear Regression Model
# Initialize the Linear Regression model
model = LinearRegression()
# Fit the model on the training data
model.fit(X_train, y_train)
# Print the coefficients and intercept
print('Coefficients:', model.coef_)
print('Intercept:', model.intercept_)- Evaluate the Model
# Predict on the test set
y_pred = model.predict(X_test)
# Evaluate the model using Mean Squared Error and R-squared
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')- Plot Predictions vs Actual Values
plt.scatter(y_test, y_pred)
plt.xlabel('Actual Median House Value')
plt.ylabel('Predicted Median House Value')
plt.title('Actual vs Predicted Values')
plt.show()example + codes in R (expand to see)
We’ll use the mtcars dataset, which is built into R and contains various features of cars, including miles per gallon (mpg), horsepower, weight, and more. We’ll build a multiple linear regression model to predict the mpg (miles per gallon) based on other features such as horsepower (hp), weight (wt), and number of cylinders (cyl).
- Load the Dataset
# Load the dataset
data(mtcars)
# View the first few rows of the dataset
head(mtcars)- Exploratory Data Analysis (EDA)
# Summary statistics of the dataset
summary(mtcars)
# Pair plot to visualize relationships
pairs(mtcars[, c("mpg", "hp", "wt", "cyl")], main = "Scatterplot Matrix")- Split the Data into Training and Testing Sets
We’ll split the data into a training set (80%) and a testing set (20%).
# Set seed for reproducibility
set.seed(123)
# Load required library
library(caTools)
# Split the data into 80% training and 20% testing
split <- sample.split(mtcars$mpg, SplitRatio = 0.8)
train_data <- subset(mtcars, split == TRUE)
test_data <- subset(mtcars, split == FALSE)
# Check the dimensions of the training and testing data
dim(train_data)
dim(test_data)- Train the Multiple Linear Regression Model
We’ll build a regression model to predict mpg using hp (horsepower), wt (weight), and cyl (number of cylinders).
# Train the multiple linear regression model
model <- lm(mpg ~ hp + wt + cyl, data = train_data)
# Summary of the model
summary(model)- Evaluate the Model’s Performance
We’ll use the testing set to evaluate how well the model performs by calculating Mean Squared Error (MSE) and R-squared values.
# Make predictions on the test set
predictions <- predict(model, test_data)
# Calculate Mean Squared Error (MSE)
mse <- mean((test_data$mpg - predictions)^2)
# Calculate R-squared
rsquared <- 1 - sum((test_data$mpg - predictions)^2) / sum((test_data$mpg - mean(test_data$mpg))^2)
cat("Mean Squared Error:", mse, "\n")
cat("R-squared:", rsquared, "\n")- Plot Actual vs Predicted Values
# Plot actual vs predicted values
plot(test_data$mpg, predictions,
xlab = "Actual MPG",
ylab = "Predicted MPG",
main = "Actual vs Predicted MPG")
abline(0, 1, col = "red")Discover more from Science Comics
Subscribe to get the latest posts sent to your email.