




























Instead of using a p‑value, you compare your test statistic (like a z‑score or t‑score) to a critical value that marks the boundary of the rejection region.
If your test statistic falls beyond the critical value → reject .
If it falls inside the non‑rejection region → fail to reject .
It’s like checking whether your result is “extreme enough” to count as evidence.
The Steps
1. State the hypotheses
Example:
2. Choose a significance level 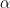
Common: 0.05, 0.01, 0.10.
3. Find the critical value(s)
Depends on:
- the test (z or t)
- whether it’s one‑tailed or two‑tailed
- the chosen
4. Compute the test statistic
Example for a t‑test:
5. Compare test statistic to critical value
- If
→ reject
- Otherwise → fail to reject
⭐ Example 1: Two‑Tailed t‑Test (Mean Difference)
A company claims the average weight of their cereal boxes is 500 g.
You sample 16 boxes:
Test:
Step 1: Choose 
Step 2: Critical value
Two‑tailed, df = 15 →
Step 3: Compute test statistic
Step 4: Compare
Decision: Fail to reject  .
.
No significant evidence that the mean differs from 500 g.
⭐ Example 2: One‑Tailed z‑Test (Proportion)
A website claims 40% of visitors click the “Subscribe” button.
You sample 200 visitors and find 38% clicked.
Test:
Step 1: 
Step 2: Critical value
One‑tailed →
Step 3: Compute test statistic
Step 4: Compare
Decision: Fail to reject  .
.
Not enough evidence that the true click rate is lower than 40%.
⭐ Example 3: One‑Tailed t‑Test (Before/After)
A teacher believes a new study technique increases test scores.
Differences (after − before) for 10 students give:
Test:
Step 1: 
Step 2: Critical value
One‑tailed, df = 9 →
Step 3: Compute test statistic
Step 4: Compare
Decision: Reject  .
.
Evidence suggests the study technique improves scores.
Why students like the critical‑value method
It feels visual and rule‑based:
- Draw the distribution
- Mark the rejection region
- Drop the test statistic in
- See where it lands
It’s like checking whether your result crosses a finish line.