Real, Imaginary, and Complex Numbers

Real numbers are all the numbers you can find on a number line, while imaginary numbers are derived from the square roots of negative numbers.

---

Real Numbers ()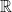

Real numbers are any values that can be plotted on a number line. They include two main categories:

• Rational Numbers: Any number that can be expressed as a fraction where . This includes:
  • Integers: …, -3, -2, -1, 0, 1, 2, 3, …
  • Fractions: ,
  • Terminating and Repeating Decimals: 0.75 (which is ) and 0.333… (which is ).
• Irrational Numbers: Numbers that cannot be expressed as a simple fraction. Their decimal forms go on forever without a repeating pattern.
  • Examples: Pi (), the square root of 2 (), and Euler’s number ().

---

Imaginary Numbers

Imaginary numbers were created to solve equations that have no real-number solution. They are based on the imaginary unit, denoted by the symbol .

This is considered “imaginary” because you can’t take the square root of a negative number in the real number system. By definition, . An imaginary number is simply a real number multiplied by .

• Examples:
  • 
  • 
  • 
  • 

Imaginary numbers are essential in many fields, including electrical engineering, physics, and signal processing. 💡

---

Complex Numbers ()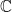

When you combine a real number and an imaginary number, you get a complex number. They are written in the form , where:

• is the real part.
• is the imaginary part.

Examples:

• 
• 
• 

Essentially, all real numbers and all imaginary numbers are types of complex numbers. For example, the real number 7 can be written as , and the imaginary number can be written as .

arithmetic operations on complex numbers

You can perform standard arithmetic operations on complex numbers by treating the imaginary unit like a variable, with the key rule that .

---

Addition and Subtraction

To add or subtract complex numbers, you combine the real parts and the imaginary parts separately.

General Form:

• Addition:
• Subtraction:

Examples:

• 
• 
• 
• 

---

Multiplication

To multiply complex numbers, use the FOIL (First, Outer, Inner, Last) method, then substitute and simplify.

Example 1:

1. FOIL:
2. Combine & Substitute:
3. Final Answer:

Example 2:

1. FOIL:
2. Combine & Substitute:
3. Final Answer:

---

Division

To divide complex numbers, multiply the numerator and the denominator by the complex conjugate of the denominator. The conjugate of is . This removes from the denominator.

Example 1:

1. Multiply by the conjugate ():
2. Numerator:
3. Denominator:
4. Final Answer:

Example 2:

1. Multiply by the conjugate ():
2. Numerator:
3. Denominator:
4. Final Answer: