Understanding Vector Spaces with Concrete Examples

A vector space (also known as a linear space) is a fundamental mathematical structure in linear algebra. It is a collection of objects, called vectors, which can be added together and multiplied (“scaled”) by numbers, called scalars. Scalars are usually real numbers, but they can also belong to other fields, like complex numbers.

Applications of vector spaces are extensive and varied across multiple fields. In physics, vector spaces play a crucial role in representing forces, velocities, and other physical quantities, allowing for an efficient mathematical framework to model complex physical phenomena such as motion, equilibrium, and electromagnetism. By using vector notation, physicists can easily analyze interactions and transformations of these quantities in different frames of reference. In the realm of artificial intelligence, vector spaces are foundational in creating vector embeddings and feature spaces, which enable models to capture similarities and differences between data points. These representations facilitate tasks such as clustering, classification, and regression, significantly improving the performance of algorithms. In computer graphics, the representation of points, transformations, and operations in 3D space relies heavily on vector spaces. Through the use of vectors, graphic designers can manipulate objects, calculate lighting effects, and integrate animations seamlessly, making vector spaces an essential tool in creating realistic simulations and visual experiences.

Definition:

A vector space $V$ over a field $F$ (e.g., $F$ could be $\mathbb{R}$ or $\mathbb{C}$ ) must satisfy the following properties:

1. Vector Addition:

If $u, v \in V$ , then $u + v \in V$ .
Addition is commutative: $u + v = v + u$ .
Addition is associative: $(u + v) + w = u + (v + w)$ .
There exists a zero vector $0 \in V$ such that $v + 0 = v$ for all $v \in V$ .
Each vector $v \in V$ has an additive inverse $-v$ such that $v + (-v) = 0$ .

2. Scalar Multiplication:

If $c \in F$ (a scalar) and $v \in V$ , then $c \cdot v \in V$ .
Distributive properties:
- $c \cdot (u + v) = c \cdot u + c \cdot v$ .
- $(c + d) \cdot v = c \cdot v + d \cdot v$ , for $c, d \in F$ .
Associativity: $c \cdot (d \cdot v) = (c \cdot d) \cdot v$ .
Identity element: $1 \cdot v = v$ , where $1$ is the multiplicative identity in $F$ .

Examples of Vector Spaces:

Euclidean Space:

$\mathbb{R}^n$ , the set of all $n$ -tuples of real numbers, is a vector space over $\mathbb{R}$ .
Example: $\mathbb{R}^2$ (2D space) or $\mathbb{R}^3$ (3D space).

Polynomial Space:

The set of all polynomials of degree $\leq n$ , with coefficients in $\mathbb{R}$ , forms a vector space.

Matrix Space:

The set of all $m \times n$ matrices with entries from $\mathbb{R}$ is a vector space.

Function Space:

The set of all continuous functions $f : \mathbb{R} \to \mathbb{R}$ forms a vector space.

**Detailed Example: *Euclidean space 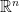$\mathbb{R}^n$ is a vector space

To show that Euclidean space $\mathbb{R}^n$ is a vector space, we need to verify that it satisfies all the properties required in the definition of a vector space over the field of real numbers $\mathbb{R}$ . The elements of $\mathbb{R}^n$ are vectors of the form:

$\mathbf{v} = (v_1, v_2, \dots, v_n),$
where $v_i \in \mathbb{R}$ for all $i$ , and $n$ is a positive integer.

We will verify each vector space property step by step.

1. Closure under Addition

For any two vectors $\mathbf{u} = (u_1, u_2, \dots, u_n)$ and $\mathbf{v} = (v_1, v_2, \dots, v_n)$ in $\mathbb{R}^n$ , their sum is defined as:

$\mathbf{u} + \mathbf{v} = (u_1 + v_1, u_2 + v_2, \dots, u_n + v_n).$

Since the sum of two real numbers is a real number, each component of $\mathbf{u} + \mathbf{v}$ is also a real number. Thus, $\mathbf{u} + \mathbf{v} \in \mathbb{R}^n$ , proving closure under addition.

2. Closure under Scalar Multiplication

For any scalar $c \in \mathbb{R}$ and vector $\mathbf{v} = (v_1, v_2, \dots, v_n)$ , scalar multiplication is defined as:

$c \mathbf{v} = (c v_1, c v_2, \dots, c v_n).$

Since the product of a real number and a real number is also a real number, each component of $c \mathbf{v}$ is a real number. Thus, $c \mathbf{v} \in \mathbb{R}^n$ , proving closure under scalar multiplication.

3. Commutativity of Addition

For any two vectors $\mathbf{u} = (u_1, u_2, \dots, u_n)$ and $\mathbf{v} = (v_1, v_2, \dots, v_n)$ :

$\mathbf{u} + \mathbf{v} = (u_1 + v_1, u_2 + v_2, \dots, u_n + v_n),$
$\mathbf{v} + \mathbf{u} = (v_1 + u_1, v_2 + u_2, \dots, v_n + u_n).$

Since addition of real numbers is commutative ( $u_i + v_i = v_i + u_i$ ), we have:

$\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}.$

4. Associativity of Addition

For any three vectors $\mathbf{u}, \mathbf{v}, \mathbf{w} \in \mathbb{R}^n$ , where:

$\mathbf{u} = (u_1, u_2, \dots, u_n), \, \mathbf{v} = (v_1, v_2, \dots, v_n), \, \mathbf{w} = (w_1, w_2, \dots, w_n),$

we check that addition is associative:

$(\mathbf{u} + \mathbf{v}) + \mathbf{w} = (u_1 + v_1 + w_1, u_2 + v_2 + w_2, \dots, u_n + v_n + w_n),$
$\mathbf{u} + (\mathbf{v} + \mathbf{w}) = (u_1 + (v_1 + w_1), u_2 + (v_2 + w_2), \dots, u_n + (v_n + w_n)).$

Since addition of real numbers is associative ( $(a + b) + c = a + (b + c)$ ), we have:

$(\mathbf{u} + \mathbf{v}) + \mathbf{w} = \mathbf{u} + (\mathbf{v} + \mathbf{w}).$

5. Existence of the Zero Vector

The zero vector in $\mathbb{R}^n$ is defined as:

$\mathbf{0} = (0, 0, \dots, 0).$

For any vector $\mathbf{v} = (v_1, v_2, \dots, v_n)$ , we have:

$\mathbf{v} + \mathbf{0} = (v_1 + 0, v_2 + 0, \dots, v_n + 0) = (v_1, v_2, \dots, v_n) = \mathbf{v}.$

Thus, the zero vector exists and satisfies the required property.

6. Existence of Additive Inverses

For any vector $\mathbf{v} = (v_1, v_2, \dots, v_n)$ , the additive inverse is defined as:

$-\mathbf{v} = (-v_1, -v_2, \dots, -v_n).$

We verify that:

$\mathbf{v} + (-\mathbf{v}) = (v_1 + (-v_1), v_2 + (-v_2), \dots, v_n + (-v_n)) = (0, 0, \dots, 0) = \mathbf{0}.$

Thus, the additive inverse exists for every vector.

7. Distributive Properties

We need to verify two distributive laws for scalar multiplication:

$c (\mathbf{u} + \mathbf{v}) = c \mathbf{u} + c \mathbf{v}$ :

$c (\mathbf{u} + \mathbf{v}) = c (u_1 + v_1, u_2 + v_2, \dots, u_n + v_n) = (c u_1 + c v_1, c u_2 + c v_2, \dots, c u_n + c v_n),$
$c \mathbf{u} + c \mathbf{v} = (c u_1, c u_2, \dots, c u_n) + (c v_1, c v_2, \dots, c v_n) = (c u_1 + c v_1, c u_2 + c v_2, \dots, c u_n + c v_n).$

Thus, $c (\mathbf{u} + \mathbf{v}) = c \mathbf{u} + c \mathbf{v}$ .

$(c + d) \mathbf{v} = c \mathbf{v} + d \mathbf{v}$ :

$(c + d) \mathbf{v} = ((c + d) v_1, (c + d) v_2, \dots, (c + d) v_n),$
$c \mathbf{v} + d \mathbf{v} = (c v_1, c v_2, \dots, c v_n) + (d v_1, d v_2, \dots, d v_n) = (c v_1 + d v_1, c v_2 + d v_2, \dots, c v_n + d v_n).$

Thus, $(c + d) \mathbf{v} = c \mathbf{v} + d \mathbf{v}$ .

8. Compatibility of Scalar Multiplication with Field Multiplication

For any scalars $c, d \in \mathbb{R}$ and vector $\mathbf{v} \in \mathbb{R}^n$ :

$c (d \mathbf{v}) = c (d v_1, d v_2, \dots, d v_n) = (c d v_1, c d v_2, \dots, c d v_n),$
$(cd) \mathbf{v} = (cd v_1, cd v_2, \dots, cd v_n).$

Thus, $c (d \mathbf{v}) = (cd) \mathbf{v}$ .

Conclusion

Since all the vector space properties are satisfied, the Euclidean space $\mathbb{R}^n$ is a vector space over the field of real numbers $\mathbb{R}$ .

Detailed Example: a function space is a vector space

To show that a function space is a vector space, we must verify that it satisfies the properties of a vector space.

The function space refers to a set of functions defined on a domain $D$ with values in a field $F$ (commonly $\mathbb{R}$ or $\mathbb{C}$ ).

For example:

Let $V$ be the set of all real-valued functions $f: D \to \mathbb{R}$ , where $D \subseteq \mathbb{R}$ .
Scalars are real numbers $\mathbb{R}$ , and vector operations (addition and scalar multiplication) are defined as:
Addition: $(f + g)(x) = f(x) + g(x)$ , for all $x \in D$ .
Scalar Multiplication: $(c f)(x) = c \cdot f(x)$ , where $c \in \mathbb{R}$ and $f(x) \in \mathbb{R}$ .

Now, we verify the vector space properties for the function space.

1. Closure under Addition

For any two functions $f$ and $g$ in $V$ , define their sum as:

$(f + g)(x) = f(x) + g(x), \quad \forall x \in D.$

Since $f(x) \in \mathbb{R}$ and $g(x) \in \mathbb{R}$ , the sum $f(x) + g(x) \in \mathbb{R}$ . Hence, $f + g \in V$ .

2. Closure under Scalar Multiplication

For any scalar $c \in \mathbb{R}$ and function $f \in V$ , define scalar multiplication as:

$(c f)(x) = c \cdot f(x), \quad \forall x \in D.$

Since $f(x) \in \mathbb{R}$ and $c \in \mathbb{R}$ , the product $c \cdot f(x) \in \mathbb{R}$ . Hence, $c f \in V$ .

3. Commutativity of Addition

For any two functions $f, g \in V$ , we have:

$(f + g)(x) = f(x) + g(x) = g(x) + f(x) = (g + f)(x).$

Thus, $f + g = g + f$ , proving commutativity.

4. Associativity of Addition

For any three functions $f, g, h \in V$ , we have:

$((f + g) + h)(x) = (f + g)(x) + h(x) = (f(x) + g(x)) + h(x),$
$(f + (g + h))(x) = f(x) + (g + h)(x) = f(x) + (g(x) + h(x)).d$

Since addition of real numbers is associative, we get:

$(f(x) + g(x)) + h(x) = f(x) + (g(x) + h(x)).$

Thus, $(f + g) + h = f + (g + h)$ , proving associativity.

5. Existence of the Zero Vector

The zero function $0 \in V$ is defined as:

$0(x) = 0, \quad \forall x \in D.$

For any $f \in V$ , we have:

$(f + 0)(x) = f(x) + 0 = f(x), \quad \forall x \in D.$

Thus, $f + 0 = f$ , proving the existence of the zero vector.

6. Existence of Additive Inverses

For any $f \in V$ , define the additive inverse $-f \in V$ as:

$(-f)(x) = -f(x), \quad \forall x \in D.$

We check:

$(f + (-f))(x) = f(x) + (-f(x)) = 0, \quad \forall x \in D.$

Thus, $f + (-f) = 0$ , proving the existence of an additive inverse.

7. Distributive Properties

We check two distributive properties for scalar multiplication:

Scalar Distributivity with Vector Addition:
For any $c \in \mathbb{R}$ and $f, g \in V$ : $c (f + g)(x) = c (f(x) + g(x)) = c f(x) + c g(x) = (c f + c g)(x).$ Hence, $c (f + g) = c f + c g$ .
Scalar Distributivity with Scalar Addition:
For any $c, d \in \mathbb{R}$ and $f \in V$ : $(c + d) f(x) = (c + d) \cdot f(x) = c f(x) + d f(x) = (c f + d f)(x).$ Hence, $(c + d) f = c f + d f$ .

8. Compatibility of Scalar Multiplication with Field Multiplication

For any scalars $c, d \in \mathbb{R}$ and $f \in V$ , we have:

$c (d f)(x) = c (d f(x)) = (c d) f(x)$

Thus, $c (d f) = (c d) f$ .

9. Existence of Scalar Identity

For any $f \in V$ , the scalar $1 \in \mathbb{R}$ satisfies:

$(1 f)(x) = 1 \cdot f(x) = f(x), \quad \forall x \in D.$

Thus, $1 f = f$ , proving the scalar identity property.

Conclusion

Since all the vector space axioms are satisfied, the function space $V$ , consisting of all real-valued functions $f: D \to \mathbb{R}$ , is a vector space over the field of real numbers $\mathbb{R}$ .

Discover more from Science Comics

Subscribe to get the latest posts sent to your email.

Understanding Vector Spaces with Concrete Examples

Definition:

1. Vector Addition:

2. Scalar Multiplication:

Examples of Vector Spaces:

**Detailed Example: *Euclidean space $\mathbb{R}^n$ is a vector space

1. Closure under Addition

2. Closure under Scalar Multiplication

3. Commutativity of Addition

4. Associativity of Addition

5. Existence of the Zero Vector

6. Existence of Additive Inverses

7. Distributive Properties

8. Compatibility of Scalar Multiplication with Field Multiplication

Conclusion

Detailed Example: a function space is a vector space

1. Closure under Addition

2. Closure under Scalar Multiplication

3. Commutativity of Addition

4. Associativity of Addition

5. Existence of the Zero Vector

6. Existence of Additive Inverses

7. Distributive Properties

8. Compatibility of Scalar Multiplication with Field Multiplication

9. Existence of Scalar Identity

Conclusion

Like this:

Related

Discover more from Science Comics

Like this:

Like this:

Like this:

Leave a ReplyCancel reply

Definition:

1. Vector Addition:

2. Scalar Multiplication:

Examples of Vector Spaces:

Detailed Example: Euclidean space* is a vector space

1. Closure under Addition

2. Closure under Scalar Multiplication

3. Commutativity of Addition

4. Associativity of Addition

5. Existence of the Zero Vector

6. Existence of Additive Inverses

7. Distributive Properties

8. Compatibility of Scalar Multiplication with Field Multiplication

Conclusion

Detailed Example: a function space is a vector space

1. Closure under Addition

2. Closure under Scalar Multiplication

3. Commutativity of Addition

4. Associativity of Addition

5. Existence of the Zero Vector

6. Existence of Additive Inverses

7. Distributive Properties

8. Compatibility of Scalar Multiplication with Field Multiplication

9. Existence of Scalar Identity

Conclusion

Share this:

Like this:

Related

Discover more from Science Comics

Related Posts

Share this:

Like this:

Share this:

Like this:

Share this:

Like this:

Leave a ReplyCancel reply

**Detailed Example: *Euclidean space $\mathbb{R}^n$ is a vector space