A one‑sample t‑test checks whether the mean of a single sample is significantly different from a known or hypothesized population mean.

It answers the question:

“Is my sample mean different enough from the population mean to rule out random chance?”

When you use it

Use a one‑sample t‑test when:

You have one group
You know or assume a population mean
You want to test whether your sample’s mean differs from that value
The data are approximately normal (especially for small samples)

Hypotheses

Two‑tailed (most common)

$H_0: \mu = \mu_0$
$H_a: \mu \neq \mu_0$

One‑tailed

$H_0: \mu \le \mu_0$ vs. $H_a: \mu > \mu_0$
or
$H_0: \mu \ge \mu_0$ vs. $H_a: \mu < \mu_0$

Fresh, Original Examples

🧪 Example 1: Vitamin C Levels

A nutritionist believes the average vitamin C level in a population is 50 mg/dL.
She measures 20 people and gets a sample mean of 54 mg/dL.

Question: Is 54 significantly different from 50?

One sample
Known population mean → one‑sample t‑test

📚 Example 2: Reading Speed

A textbook claims that the average reading speed of adults is 250 words/minute.
You test 15 students and find a mean of 230 words/minute.

Question: Are your students slower than the claimed average?

One group
Comparing to a published mean → one‑sample t‑test

🧠 Example 3: Memory Test Scores

A cognitive test is designed so that the population mean score is 100.
Your sample of 12 participants scores an average of 108.

Question: Is your group performing above the standard?

One sample
Known test mean → one‑sample t‑test

🏃 Example 4: Average Step Count

A fitness tracker company advertises that users take 8,000 steps/day on average.
You collect data from 30 users and find a mean of 7,450 steps/day.

Question: Is the real average lower than advertised?

One sample
Testing against a claimed mean → one‑sample t‑test

🎮 Example 5: Game Completion Time

A game developer says the average completion time for a level is 12 minutes.
You test 10 players and get a mean of 13.2 minutes.

Question: Are players taking longer than expected?

One sample
Known benchmark → one‑sample t‑test

Formula (for completeness)

$t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}$

Where:

$\bar{x}$ = sample mean
$\mu_0$ = hypothesized population mean
$s$ = sample standard deviation
$n$ = sample size

Fully worked one‑sample t‑test example

A company claims that their energy bars contain on average 200 calories.

You suspect the true mean is lower than 200.
You take a sample of 10 bars and measure the calories:

$196, 203, 189, 201, 195, 192, 200, 194, 190, 198$

We’ll test (one‑tailed):

$H_0: \mu = 200$
$H_a: \mu < 200$

Significance level: $\alpha = 0.05$

Step 1: Compute the sample mean 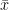$\bar{x}$

Add them up:

$196 + 203 + 189 + 201 + 195 + 192 + 200 + 194 + 190 + 198 = 1958$

Sample size: $n = 10$

$\bar{x} = \frac{1958}{10} = 195.8$

Step 2: Compute the sample standard deviation $s$

First, compute each deviation from the mean and square it:

$\begin{aligned}196 - 195.8 &= 0.2 &\Rightarrow 0.2^2 &= 0.04 \\203 - 195.8 &= 7.2 &\Rightarrow 7.2^2 &= 51.84 \\189 - 195.8 &= -6.8 &\Rightarrow (-6.8)^2 &= 46.24 \\201 - 195.8 &= 5.2 &\Rightarrow 5.2^2 &= 27.04 \\195 - 195.8 &= -0.8 &\Rightarrow (-0.8)^2 &= 0.64 \\192 - 195.8 &= -3.8 &\Rightarrow (-3.8)^2 &= 14.44 \\200 - 195.8 &= 4.2 &\Rightarrow 4.2^2 &= 17.64 \\194 - 195.8 &= -1.8 &\Rightarrow (-1.8)^2 &= 3.24 \\190 - 195.8 &= -5.8 &\Rightarrow (-5.8)^2 &= 33.64 \\198 - 195.8 &= 2.2 &\Rightarrow 2.2^2 &= 4.84 \\\end{aligned}$

Sum of squared deviations:

$0.04 + 51.84 + 46.24 + 27.04 + 0.64 + 14.44 + 17.64 + 3.24 + 33.64 + 4.84 = 199.6$

Sample variance:

$s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1} = \frac{199.6}{9} \approx 22.18$

Sample standard deviation:

$s = \sqrt{22.18} \approx 4.71$

Step 3: Compute the t‑statistic

Formula:

$t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}$

Here:

$\bar{x} = 195.8$
$\mu_0 = 200$
$s \approx 4.71$
$n = 10$

Standard error:

$SE = \frac{s}{\sqrt{n}} = \frac{4.71}{\sqrt{10}} \approx \frac{4.71}{3.162} \approx 1.49$

Now:

$t = \frac{195.8 - 200}{1.49} = \frac{-4.2}{1.49} \approx -2.82$

Step 4: Degrees of freedom and critical value

Degrees of freedom:

$df = n - 1 = 9$

For a one‑tailed test at $\alpha = 0.05$ and $df = 9$ , the critical t‑value is about:

$t_{\text{crit}} \approx -1.833$

(negative because we’re testing $\mu < 200$ ).

Step 5: Decision

Our test statistic:

$t \approx -2.82$

Compare:

$t = -2.82 < -1.833 = t_{\text{crit}}$

So the test statistic falls in the rejection region.

We reject $H_0$ at the 5% level.

Step 6: Interpretation in words

There is statistically significant evidence at $\alpha = 0.05$ that the true mean calorie content is less than 200 calories per bar.

One sample t-test

When you use it